Control Charts

Another technique for developing a process control system is Statistical Process Control (SPC).

An SPC chart is nothing more than a time-ordered graph of your process data. When these data are plotted using statistical software, the resulting graph outlines the expected extent of variation of the data. Since the expected range is known, anything outside of that is considered a special occurrence that needs investigation and correction.

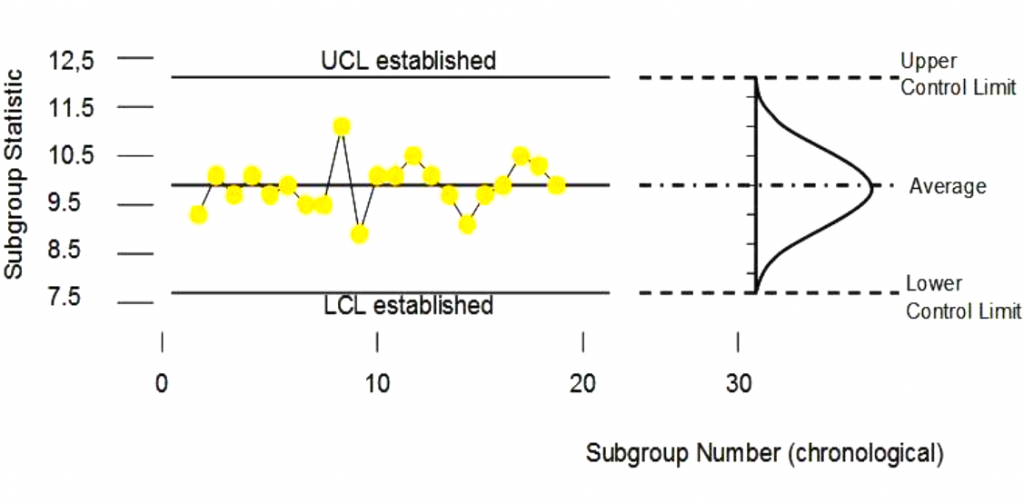
SPC charts can monitor either your process Xs, your process Y (inputs or output), or both. In the long run, SPC charts can help reduce rejects and rework, boosting productivity.

Purpose of control charts
Characteristics of control charts
Use of control charts
Creating control charts
Translate various control charts
Reacting to control charts

Statistical Process Control

Every process has two types of variation
- Inherent process variation (common cause)
- Variation due to an assignable reason (special cause)
SPC highlights common causes & special cause variation
Monitors long-term process performance – shows boundaries of acceptable performance
Used for continuous and discrete data

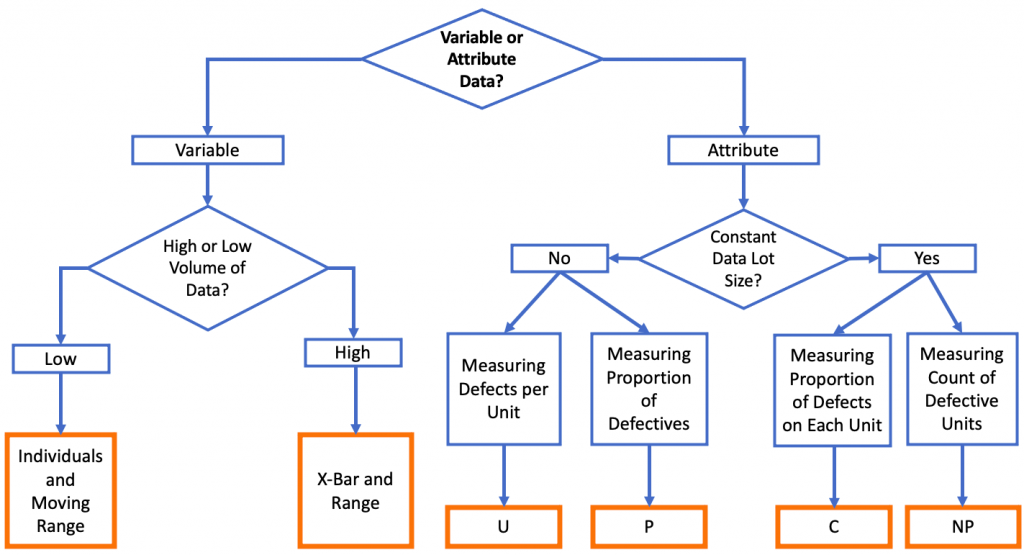
Based on your process data, you can find out what chart can be used. Once you have collected the data, you can use statistical software to produce the appropriate chart(s) and continuously monitor the process.

Individual and Moving Range Chart

Used with time-ordered data to detect the presence of special cause variation
It can be used when no rational sub-group exists, such as
- An office metric that is calculated once a day
- An expensive, destructive test is done once a shift
It consists of 2 control charts
- Individual Chart – plots individual data point
- Moving Range – plots the difference between successive points

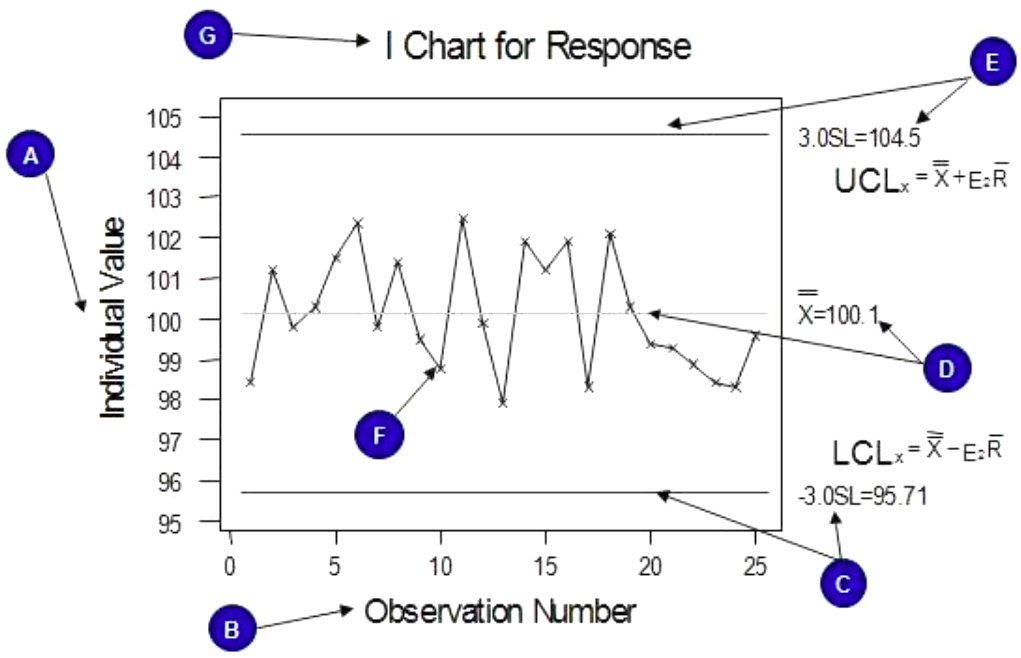
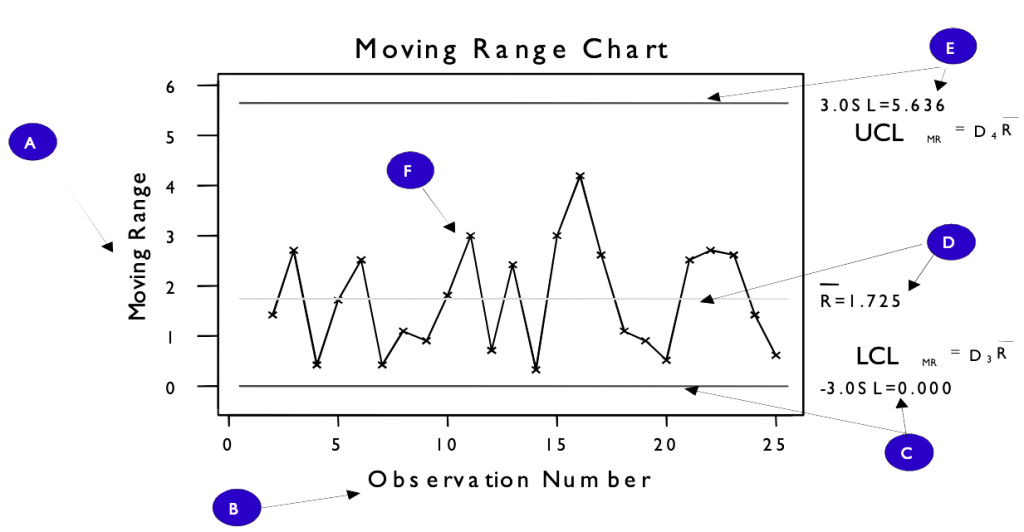
Creating an I-MR Control Chart

Choose what to measure
Plan data collection
Collect samples, record data
Plot each data point in time series – Individual Chart
Calculate the overall average of data points (Xbar)
Calculate the difference between successive points
Plot on Moving Range chart – mR Chart
Calculate the average of mR data points
Determine the control limit for ranges
- UCL=3.267 x mR
- Lower Control Limit = 0
Ranges in statistical control?
- If not – inherent variation isn’t stable
Determine control limits for individual data points
- Control Limits = X ± 3(mR/d₂)
- Control limits are based on a ‘short-term’ estimate of the standard deviation
Individual points in statistical control?
- If yes – inherent (common) cause only
- If not – some special causes affecting the process

X-bar and Range Chart

Used with time-ordered groups of data to detect short-term versus long-term variation
Used with rational sub-groups such as
- Consecutive shifts
- Samples were taken on the hour every hour
It consists of 2 control charts
- Xbar Chart – plots averages for each sub-group
- Range Chart – plots range (max/min) within each sub-group

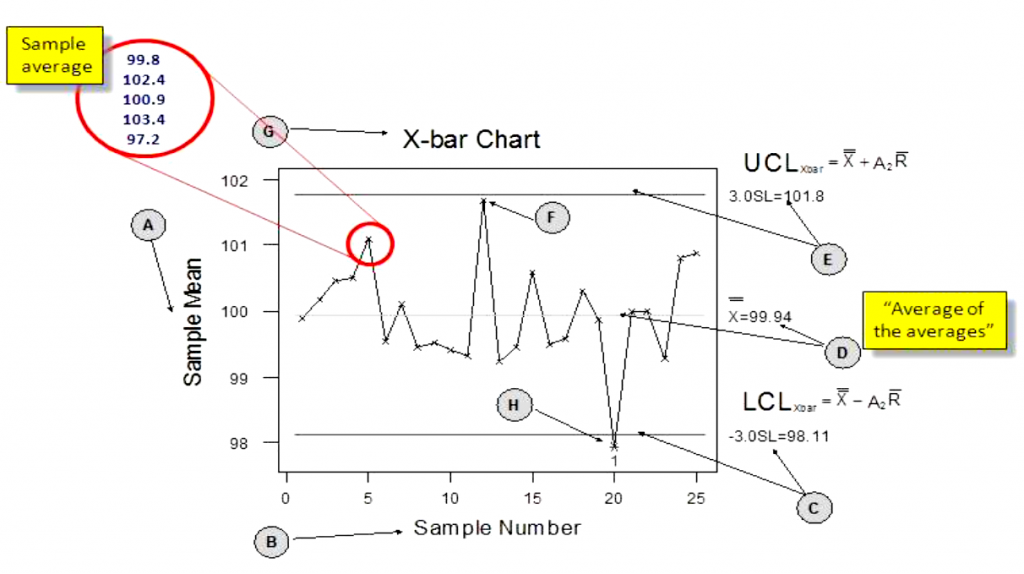
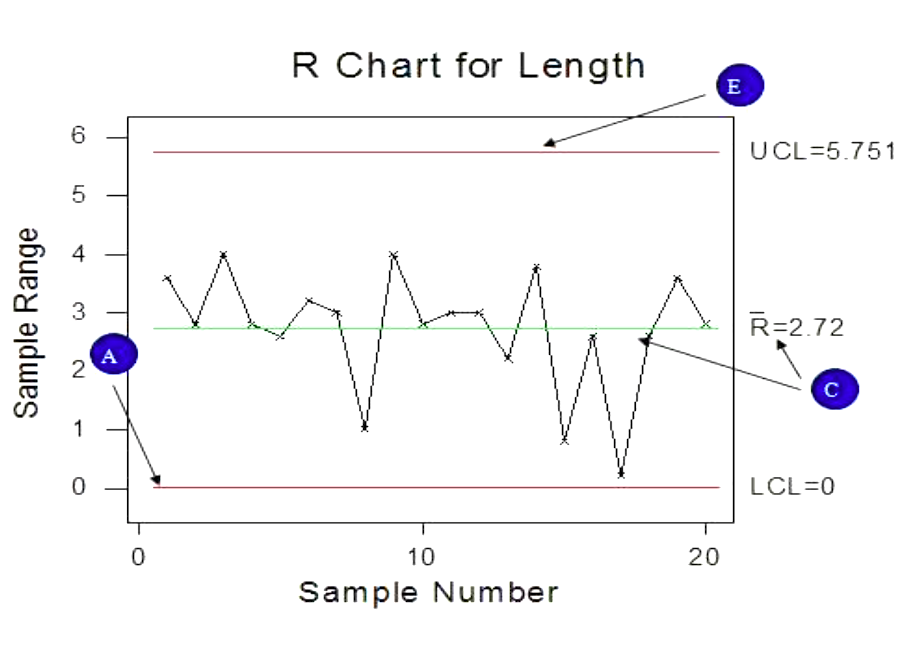
Creating an X-bar and R Control Chart

Choose what to measure
Plan data collection
Collect samples, record data
Calculate the average for each sub-group and plot in time series – Xbar Chart
Calculate the overall average of Xbar Chart X
Calculate the range for each sub-group and plot on Range Chart – R Chart
Calculate the average of R Chart R
Determine the control limit for ranges
- UCL=D₄ x R
- LCL=D₃ x R
Ranges in statistical control?
- If not – variation exists within sub-group
Determine control limits for averages
- Control Limits = X + A₂ R
Averages in statistical control?
- If yes – inherent (common) cause only
- If not – variation exists between sub-groups

Attribute Control Charts

Set of control charts specifically designed for discrete or attribute data
Seek to determine if the rate of non-conforming items (errors) is stable and detect when a deviation from the stable state has occurred
The number of non-conforming items (errors) or conforming items may be plotted

Considerations for Attribute Charts

Sample Size of Subgroup
- A sample size of each subgroup must be large enough to ensure there is at least one defect per subgroup
- A lower rate of defects in the process will require a larger sample size to monitor and detect changes
Number of Data Points
- In most cases, attribute charts need at least 50 data points

u-Chart (Defect/Unit)

The number of defects per unit (u) is calculated for each subgroup as the total number of defects (c) in the subgroup of size n
These defects per unit are plotted on the control chart
This chart does not require an equal subgroup size
The average of the chart is calculated as:
- ubar = sum of all defects divided by the number of data points in all subgroups
The control limits of the chart are calculated as:
- UCL = ubar + 3 √ubar/n
- LCL = ubar – 3 √ubar/n

p-Charts (Percentage of Defectives)

The percentage of defectives are calculated for each subgroup
This percentage of defectives is plotted on the control chart
This chart does not require an equal subgroup size
The average of the chart is calculated as:
- pbar = sum of all defectives divided by the number of data points in all subgroups
The control limits of the chart are calculated as:
- UCL = pbar + 3 √ ((pbar(1 – pbar))/n
- LCL = pbar – 3 √ ((pbar(1 – pbar))/n

c-Charts (Count of Defects)

The number of defects is counted for each subgroup
This count of defects is plotted on the control chart
This chart requires equal subgroup size – the same number of data points per subgroup
The average of the chart is calculated as:
- cbar = sum of all defects divided by the number of subgroups
The control limits of the chart are calculated as:
- UCL = cbar + 3 √ cbar
- LCL = cbar – 3 √ cbar

np-Charts (Count of Defectives)

This number of defectives is plotted on the control chart
This chart does require an equal subgroup size
The average of the chart is calculated as:
- npbar = sum of all defectives divided by the total number of data points in all subgroups
The control limits of the chart are calculated as:
- UCL = npbar + 3 √(npbar(1 – npbar)
- LCL = npbar – 3 √(npbar(1 – npbar)

Summary – Control Charts

Report long-term capability
Insight into what the process is doing
Focus on consistent quality
Enables targeting to specification
Fire prevention vs. Fire fighting
Often part of the process baseline in the Measure Phase and also the Control Plan