Process improvement is a critical aspect of any organization, and understanding key statistical concepts like average, variation, and capability can help drive more efficient and effective decision-making. This article will explore these concepts, their calculations, and their applications in understanding and improving processes.
Section 1: Average and Variation – The Basics
Average, also known as the mean, is a measure of central tendency representing the sum of all data points divided by the total number of data points. It is a useful metric to understand a dataset’s “typical” value.
Conversely, variation measures the dispersion or spread of the data points in a dataset. It helps us understand how consistently a process performs. A common measure of variation is the standard deviation, which can be calculated using the following formula:
Standard Deviation (σ) = √(Σ(x – μ)² / N)
where x represents each data point, μ is the mean of the dataset, and N is the total number of data points.
Section 2: Capability – An Overview
Capability measures how well a process meets the specified limits or requirements. It is a critical metric in process improvement and quality management. Two commonly used capability indices are Cp and Cpk.
Cp (Process Capability) is calculated using the following formula:
Cp = (USL – LSL) / (6 * σ)
where USL and LSL are the upper and lower specification limits, respectively, and σ is the process standard deviation.
Cpk (Process Capability Index) is calculated using the following formula:
Cpk = min[(USL – μ) / (3 * σ), (μ – LSL) / (3 * σ)]
Cpk considers both the process variation and its mean, making it a more informative metric compared to Cp.
Section 3: Using Cp and Cpk to Understand a Process
Cp and Cpk are used to evaluate the capability of a process and determine if it meets the specified limits. A higher Cp or Cpk value indicates a more capable process. Generally, a Cp or Cpk value of 1.33 or higher is considered acceptable, indicating that the process is capable of meeting the requirements within the specified limits.
By comparing Cp and Cpk, we can understand if the process is centred within the specification limits. The process is centred if Cp and Cpk are equal or very close. If Cpk is significantly lower than Cp, it suggests that the process is off-center, and improvement actions may be needed.
Section 4: Converting Cp and Cpk to Percent of Failure
Cp and Cpk can be converted to percent of failure, which estimates the percentage of defective products produced by the process. To do this, we first convert the Cp or Cpk value to the corresponding Z-score using the following formula:
Z = Cp * 3 (for Cp) or Z = Cpk * 3 (for Cpk)
Next, we use the Z-score to determine the area under the standard normal distribution curve, representing the product percentage within the specification limits. The percentage of failure can then be calculated as follows:
Percent of Failure = (1 – Area under the curve) * 100
This way, Cp and Cpk can estimate the risk of producing defective products and help prioritize improvement efforts.
Applying and comprehending crucial statistical concepts, such as average, variation, and capability, is essential for organizations to enhance their processes and make well-informed decisions. Companies can assess process performance, pinpoint areas for improvement, and reduce the possibility of producing faulty products by utilizing metrics such as Cp and Cpk. Embracing these concepts will result in improved efficiency, superior quality, and increased customer satisfaction. As you carry on analyzing and enhancing your processes, it is advisable to incorporate these indispensable tools into your quality management and continuous improvement efforts. Wishing you the best in your analysis!
4M Analysis Process
The purpose of this procedure is to define the steps to do a 4M …
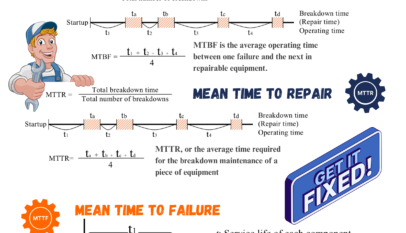
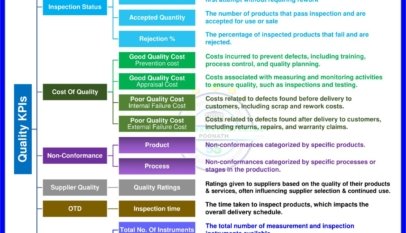
Good learning platform here.
Can able learn lot of things in here who are willing to growth up in career.
Nice study platform.