Introduction to Hypothesis Testing

Hypothesis Testing is a statistical tool, that allows the resemblance of two or more process attributes – mean, median, and standard deviation. It provides a method to determine differences.

• An important part of a conclusion reached based on random sampling (statistical inference)
  • A hypothesis is a statement we want to verify using data
    • is there a difference?
    • has there been a change?
• Null and Alternative hypotheses are formed
  • Level of risk and confidence required
• Experimentation is conducted, and interpret the results
  • Fail to reject the null hypothesis
    • No change. No difference, or…
  • Reject the null hypothesis
    • There is a change, a difference

What might we “Test” for?

We will be testing for a Change or Difference in Process…

• Central Tendency
  • Mean, Median, Mode
• Variation
  • Variance, Standard Deviation
• Proportion
  • % (ratio, proportion)
• Frequency (of occurrence)
  • Distribution of count/frequency

Testing Protocol

• “Null” hypothesis (H0)
  • This statement validates the status quo – no significant change will be observed. Any differences detected are purely due to chance and not a change in the process.
  • Symbols:
    • = (equals)
    • < (not less than)
    • > (not greater than)
• “Alternative” hypothesis (H1)
  • This is a statement that there will be a difference in statistical significance detected; there has been a change.
  • Symbols:
    • <> (doesn’t equal)
    • < (is less than)
    • > (is greater than)

The hypotheses are complementary to each other. If one is true, the other is not true, and vice versa.

If the p is low, the null must go!

When performing any statistical test, the outcome is based on sampling from the population; therefore, there is room for error. Most statistical tests are run with a 95% confidence level, indicating a 5% chance of making an error.

The decision to accept or reject the null hypothesis is predicated on the calculated p value. If the p value is a smaller amount than or adequate to a preassigned significance level (normally set at 5%), then we reject the null hypothesis and accept the alternative.

A p value will be calculated by the statistical software when running a hypothesis test.

Types of Hypothesis Testing

There are many different types of hypothesis tests, and they can be divided into two main categories:

• Parametric tests
  • Makes inferences about parameters like mean and variance
  • Based on assumptions of specific distributions (ex. “normal” or “t” distributions)
• Non-parametric tests
  • Makes inferences about frequency distribution like median, distribution type
  • Usually include sign and rank tests (a type of “math” used)
  • Do not require normality assumptions (but have some assumptions… always check them!)

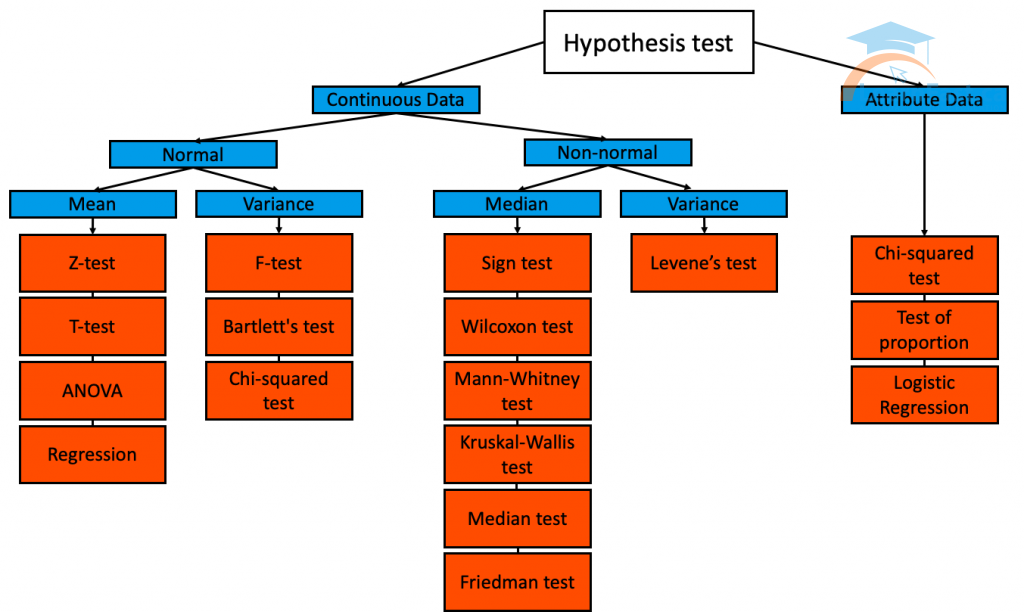
Depending on the type of data you have collected, and whether it’s normal or non-normal, several hypothesis tests are available for comparing process characteristics.