1. The Thinking behind Focused Improvement
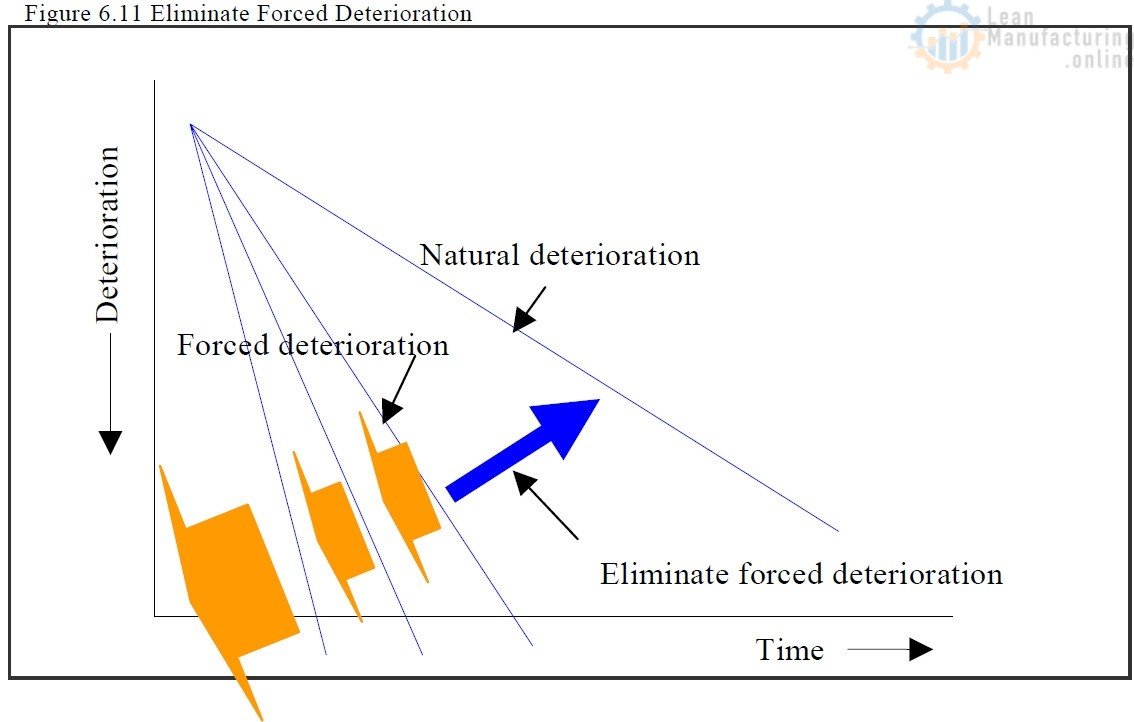
The effects of much conventional improvement activity used to be transitory, and there was a strong tendency for improvements not to be capable of being sustained or properly established. In TPM, by contrast, activities are organised to ensure that the benefits of Focused Improvements are upheld, principally through Autonomous Maintenance.
1.1 The Basic Thinking behind Focused Improvement
1.2 Allocating Roles in Focused Improvement
1.3 Planning for Focused Improvement
1.4 Rolling Out Focused Improvement Step by Step
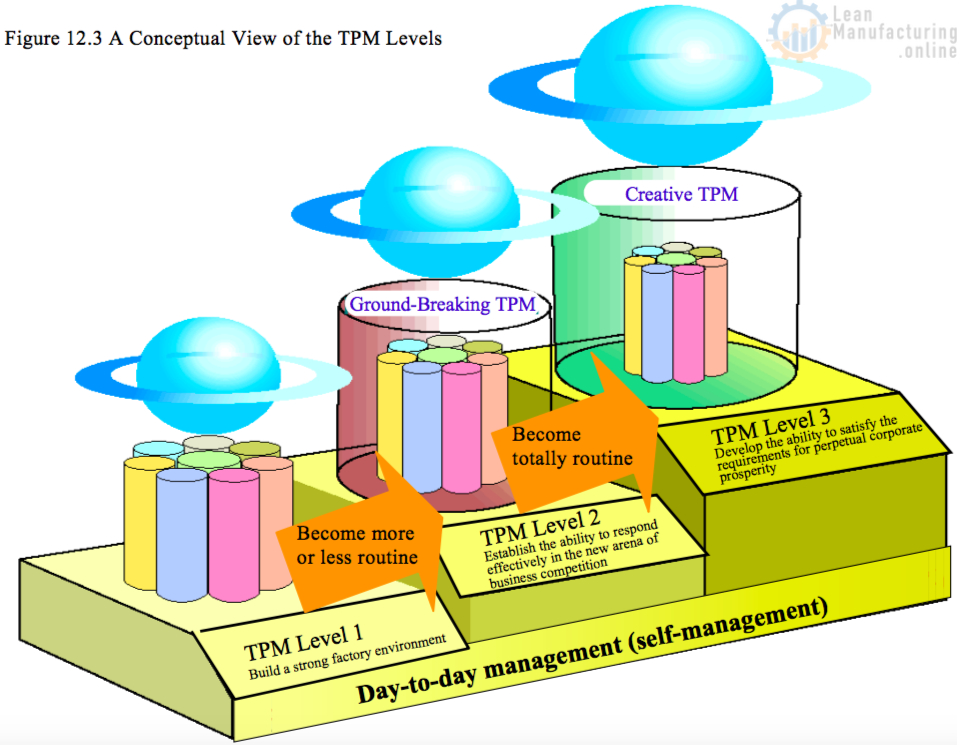
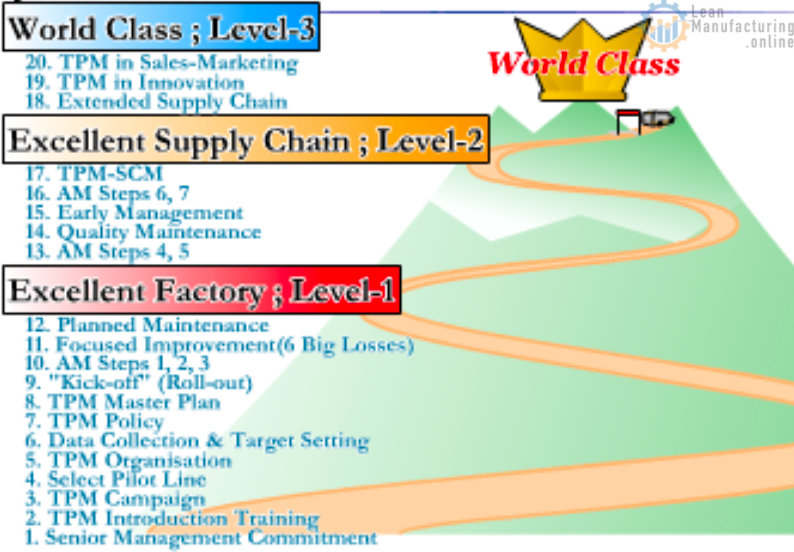
2. How Effectively Are Losses being Tackled? – A 4-Level Assessment
3. Tools and Techniques for Focused Improvement
4. The QC Story
5. The 7 QC Tools and the 7 New QC Tools
Quality control needs to be based on facts rather than experience or intuition. The original purpose of quality control was to reduce the number of product defects in mass production, and their chief cause was thought to be variability, so statistical tools were used to address the problem.
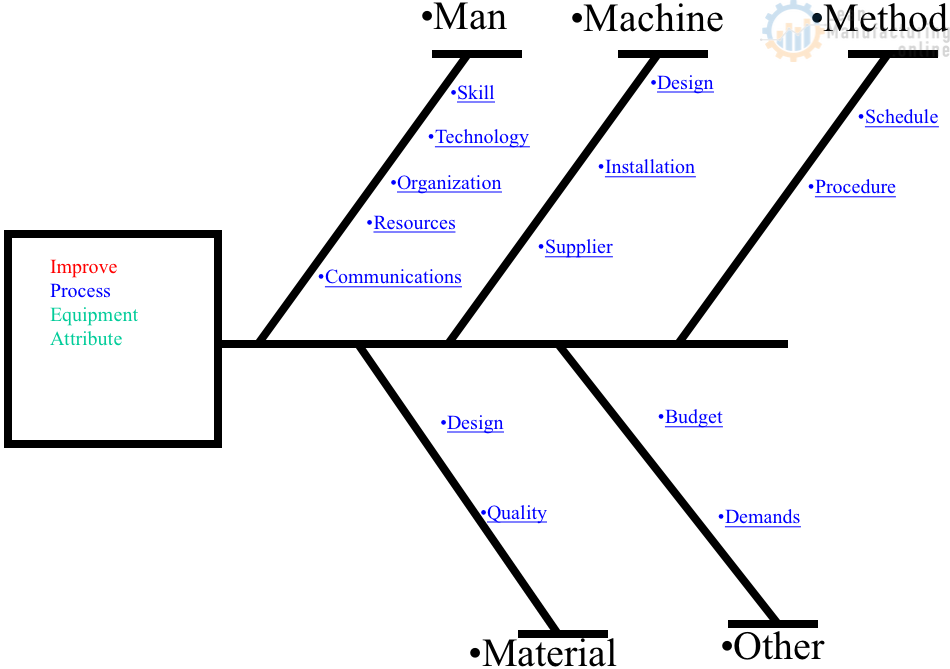
Statistical tools used in quality control include control charts, histograms, Pareto diagrams, design of experiments, and sampling inspection. Non-statistical approaches are also used, in the form of cause-and-effect diagrams, QFD (quality function deployment), FMEA (failure mode and effects analysis) and FTA (fault-tree analysis), among others. These methods focus on graphic representation of data likely to prove useful in solving the problem, and their advantage is that they make the problem visible.
In contrast to the traditional 7 QC Tools explained in section 5.2, which are used to handle numerical data, the 7 New QC Tools are used mainly for analysing verbal data. They consist of relations diagrams, tree diagrams, matrix diagrams, process decision programme charts, arrow diagrams, affinity diagrams, and matrix data analysis.
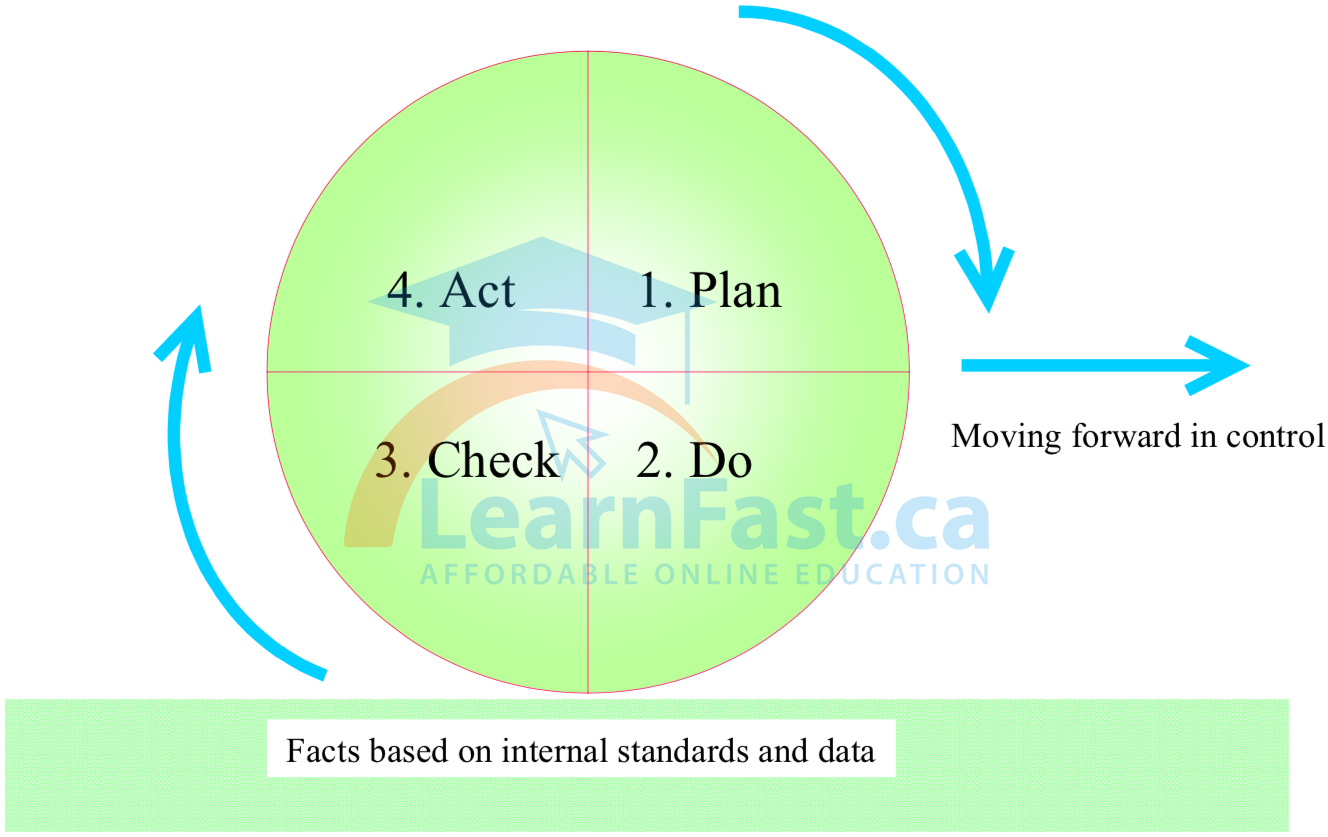
5.1 Control
Control makes it possible to achieve a planned value for a given task. The basic approach to control is to repeat the following sequence: Plan → Do → Check (inspect/diagnose) → Act (repair/improve). This is called the ‘PDCA cycle’ or the ‘control cycle’ (see Figure 4.6).